|
FFT乗算 |
|
FFT乗算原理の確認 |
| 最終更新日:2007/02/20 修正 |
●概要
FFTは、にわかに実現するのは困難なので、原理通りのDFTで実際に確認を行った。2要素同士の乗算で確認した。
回転子は予めテーブル化してある(下表)。但し、N = 4 なので、値は単純となっている。超簡単な複素構造体と、複素乗算関数を作成し、確認した。
DFT 回転子行列
| 1 | 1 | 1 | 1 |
| 1 | -j | -1 | j |
| 1 | -1 | 1 | -1 |
| 1 | j | -1 | -j |
IDFT 回転子行列
| 1 | 1 | 1 | 1 |
| 1 | j | -1 | -j |
| 1 | -1 | 1 | -1 |
| 1 | -j | -1 | j |
表で、j は虚数単位(一応電気出身なので、どうしても j を使ってしまう)
●結果
4要素で、後半を0にして、線形化している。
○例1:11 * 11
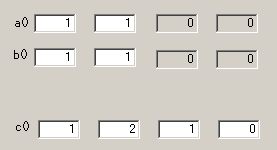
・10進数とすれば、そのまま、11 * 11 = 121 となり、正しい。
・100進数とすれば、0101 * 0101 の乗算になり、結果を2桁にすれば、
010201 となり、正しい。
○例2:1111 * 1111
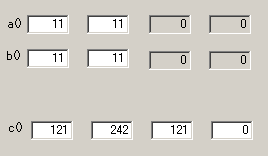
・100進数だとすれば、1111 * 1111 となる。結果を100で規格化すれば、
末尾 121 → 21とキャリーが1
真中 242 → 242 + 1 なので、43とキャリーが2
先頭 121 → 121 + 2 なので、23 とキャリーが1
結局、1234321となり、正しい。
・1000進数と思えば、011011 * 011011 となり、キャリーはないので、
そのまま 121242121 が回答となる
○例3:999999 * 999999
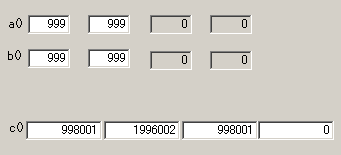
・1000進数とすれば、999999 * 999999 となる。結果を1000で規格化すれば、
末尾 998001 → 001とキャリーが998
真中 1996002 → 1996002 + 998 = 1997000なので、000とキャリーが1997
先頭 998001 → 998001 + 1997 = 999998なので、998とキャリーが999
結局、999998000001 となり、正しい。
・10000000進数とすれば、0000999|0000999 * 0000999|0000999 の乗算となり、そのままが解答となる。つまり、 結果の桁を7桁にすれば、キャリーはなく、
0998001|1996002|0998001 となり、正しい。
●判断
入力に矛盾がなければ(要素がN未満)、N進数と勝手に思えば良い。桁上げは一般的に生じるとし、常に処理する必要がある。以上、どうやらDFT乗算は本当らしい。
●コード例
上記試験に使用した、つたないコードを紹介する。
Structure WW '複素構造体
Public Re As Double
Public Im As Double
Sub New(ByVal R As Double, ByVal I As Double)
Me.Re = R
Me.Im = I
End Sub
End Structure
Dim A(), B(), C() As Double '入力データ
Dim FA(), FB(), FC() As WW 'フーリエ変換
'回転子行列(順)
Dim FW(,) As WW = { _
{New WW(1, 0), New WW(1, 0), New WW(1, 0), New WW(1, 0)} _
, {New WW(1, 0), New WW(0, -1), New WW(-1, 0), New WW(0, 1)} _
, {New WW(1, 0), New WW(-1, 0), New WW(1, 0), New WW(-1, 0)} _
, {New WW(1, 0), New WW(0, 1), New WW(-1, 0), New WW(0, -1)}}
'回転子行列(逆)
Dim RW(,) As WW = { _
{New WW(1, 0), New WW(1, 0), New WW(1, 0), New WW(1, 0)} _
, {New WW(1, 0), New WW(0, 1), New WW(-1, 0), New WW(0, -1)} _
, {New WW(1, 0), New WW(-1, 0), New WW(1, 0), New WW(-1, 0)} _
, {New WW(1, 0), New WW(0, -1), New WW(-1, 0), New WW(0, 1)}}
Private Sub btnGo_Click(ByVal sender As System.Object, ByVal e As
System.EventArgs) Handles btnGo.Click
Dim i, j As Integer
Dim W As WW
ReDim A(3)
ReDim B(3)
ReDim C(3)
A(0) = txtA0.Text
A(1) = txtA1.Text
B(0) = txtB0.Text
B(1) = txtB1.Text
ReDim FA(3)
ReDim FB(3)
ReDim FC(3)
'被乗数のDFT
For i = 0 To 3
For j = 0 To 3
W = ComplexM(New WW(A(j), 0),
FW(i, j)) 'データの虚数部は0
FA(i).Re = FA(i).Re + W.Re
FA(i).Im = FA(i).Im + W.Im
Next
Next
'乗数のDFT
For i = 0 To 3
For j = 0 To 3
W = ComplexM(New WW(B(j), 0),
FW(i, j)) 'データの虚数部は0
FB(i).Re = FB(i).Re + W.Re
FB(i).Im = FB(i).Im + W.Im
Next
Next
'コンボリューション(畳み込み)
For i = 0 To 3
FC(i) = ComplexM(FA(i), FB(i)) 'ここがミソ
Next
'結果のIDFT
For i = 0 To 3
For j = 0 To 3
W = ComplexM(FC(j), RW(i, j))
C(i) = C(i) + W.Re
'結果は実数部のみ採用
Next
C(i) = C(i) / 4
Next
txtc0.Text = C(0).ToString
txtc1.Text = C(1).ToString
txtc2.Text = C(2).ToString
txtc3.Text = C(3).ToString
End Sub
'複素乗算
Private Function ComplexM(ByVal A As WW, ByVal B As WW) As WW
ComplexM.Re = A.Re * B.Re - A.Im * B.Im
ComplexM.Im = A.Re * B.Im + B.Re * A.Im
End Function