|
ソフトウェア実験室 |
|
級数の収束速度1 |
| 最終更新:2006/01/23 修正 |
指数関数の近似値にて、紹介した方法は、関数を無限級数展開した式から近似的に求める方法である。近似的と言うが、計算方法によっては超高精度となる。とは言っても、素で勝負すると、値によっては、なかなか収束しなくなる。常識的な有限の回数で求める精度を得たいと思うはず。
ここでは、10x の関数(xは任意の非整数値)で具体的に実験してみる。
●原理
○一般
一般に、関数の級数展開は、
f(x) = Σ A(x,k)/B(x,k) [k = 0 to ∞]
と表せる。ここで、有限の大きさのk 以降で、A(x,k) < B(x,k) が成立しないといけない。A(x,k) ≪ B(x,k) が理想。また、小数点以下の精度の場合は、
|A(x,k)/B(x,k)| < 10-L
などが、精度L桁を確保するための条件となる。このとき、なるべく小さな k としたい。
○指数関数
10x は、
10x = ∑((Xln(10))k/k!) [k = 0 to ∞]
となっている。従って、(Xln(10))kと k! の比が勝負となる。この展開式では、あらゆるxで成立することになっているが、分子はxによってはかなりの大きさになる。今、x = 43.43 としてみると、分子は、100 となる。つまり、100k と k! の勝負となる。下表は、k による、分母、分子のおよそのオーダ(10の何乗か)を調べたものである。x = 43.43 では、200、300 以上が必要になりそうと分かる。
| k | 100k | k! |
| 10 | 20 | 6 |
| 50 | 100 | 64 |
| 100 | 200 | 157 |
| 200 | 400 | 374 |
| 500 | 1000 | 1134 |
| 1000 | 2000 | 2567 |
●方法
指数法則を利用して、級数の分子を小さくする。
今、AB で、B を非整数とすれば、B = I + F と表される。ここで、I は整数部分、F は小数部分とする。従って、
AB = A(I + F) = AI * AF
となる。しかし、AI は、整数の冪乗なので、単純な演算で算出できる。従って、AF の算出に帰着される。しかも、Fは、高々、1未満の比較的小さな値となる。しかも、A = 10 であれば、AI は、十進システムでは、指数の調整のみで行える。
今、1043.43 を考えると、100.43 のみを級数展開すれば良い。この場合、分子は、0.43*ln(10) = 0.99011 となる。これは、常に、オーダが0なので、上表から、例えば、50回で、64桁以上の精度が出ることが分かる。
●実験方法
1043.43 について、そのままで級数展開で計算する方法と、上記の方法での収束具合を測定する。
●結果
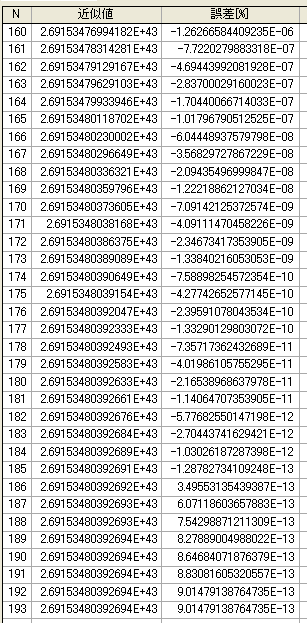
通常の方法193回で収束
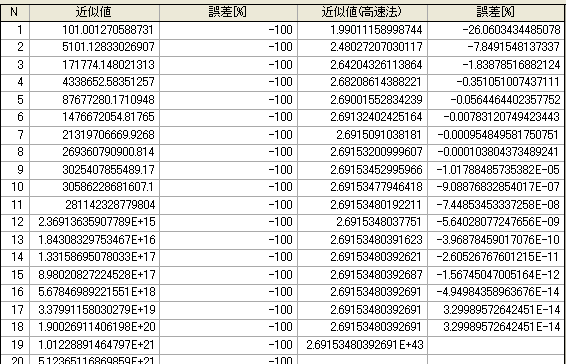
高速法の場合(右側)、18回で収束
N=19 は1043倍した最終結果を表示している。
●結論
この方式は有効である。指数の大きさに依らずに、収束速度が安定する。