|
ソフトウェア実験室 |
|
算術幾何平均でπを求める |
| 最終更新:2006/02/26 更新 |
従来、πの算出では、逆正接の展開式で求められていたが、最近では、算術幾何平均による方法が用いられてると言う。いわゆる、ガウス・ルジャンドル法である。原理については、筆者は、全く理解できないので、それには一切触れない。
●漸化式
全ての変数は、求める精度を保持できる多倍長数とする。
a = 1
b = 1 / Sqrt(2)
t = 1
X = 4
Do While 精度未満
Y = a
a =(a + b) / 2
b = Sqrt(Y * b)
t = t - X * (Y - a)2
X = X * 2
Loop
π = (a + b)2 / t
求める精度を n 桁とすれば、繰り返し回数は、Log2(n) 程度となる。26万桁なら、僅か、18回となる。
●注意
- 初期値の、b = 1 / Sqrt(2) の精度は、(どうも)求める精度以上でないといけない。
- この方式の難点は、高精度な平方根と、多くの多倍長変数が必要なことで、メモリの少ないシステムでは、辛いかもしれない。
- 所要時間は、開平時間が支配的となる。
●実験
実験に使用したコードは以下の通りである。上記、漸化式通りのベタなコードとなっている。
従来の数学関数は、Math. が接頭されている。
Dim i, LC As Integer
Dim aa As New UltraLong(1)
Dim bb As New UltraLong(Div(1, Sqrt(2)))
Dim t As New UltraLong(1)
Dim X As New UltraLong(4)
Dim Y As New UltraLong(0)
Dim Ya As New UltraLong(0)
LC = CInt(Math.Log10(Precision) / Math.Log10(2))
For i = 0 To LC - 1
Y = aa
aa = Div(Add(aa, bb), 2)
bb = Sqrt(Mul(Y, bb))
Ya = Subt(Y, aa)
t = Subt(t, Mul(X,
Mul(Ya, Ya)))
X = Mul(X, 2)
Next
Y = Div(Mul(Add(aa, bb), Add(aa, bb)), t)
●結果(2006/2/26 再測定)
→結果(ガウスの時間)がおかしいので、調べたところ、プログラムの一部にデバッグルーティンが残っていた。それを除去して再測定した。)
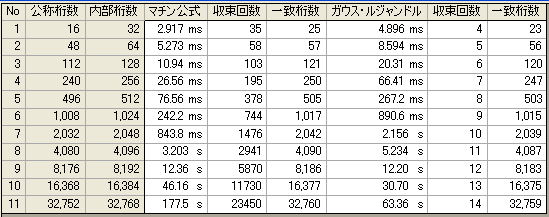
マチン公式による方法と所要時間を比較して見た。 演算時間は、それぞれ、マチン公式、ガウス・ルジャンドルと表記された欄に表示している。収束回数は、実際のループ回数、一致桁数は、正しいと思われる5万桁の π の値(ネット上に100万桁のπ値が公開されており、それを、UltaLong値に変換したもの)とUltraMathのHowEqualメソッドにて比較し、先頭から一致した桁数である。
●考察
期待に反して、ガウス・ルジャンドル法の速度はマチン公式と同じような時間となった。収束回数は非常に少ないのにこの状態となっている。この原因は、
- ガウス・ルジャンドル法では、高精度の開平と多倍長同士の乗算が多く、収束が早くても、演算時間が掛かる。
- マチン公式は、なるほど収束は遅いが、乗除算は全て、多倍長と通常の数値であり、この演算速度は、頗る速い。32,000桁の乗算では、50倍(除算では180倍 、今回は除算は無関係)の速さ。
- しかし、8千桁を超えると、ガウスの方が、目に見えて早くなっている。
●結論
- PCレベルでは(1万桁未満)、マチン公式が相応しい。
- 全く異なる方法で、同じ値を求めて、一致すると言うことは、それぞれの演算が正しいことの証明になった。